|

Pyramider och matematik

Pyramiderna har aldrig dolt kunskapen. Det är bara våra föreställningar om dem som gjort att vi inte sett den.
Gravar har det sagts oss, men när vi betraktar dem ur ett matematiskt kunskapsperspektiv framträder något häpnadsväckande.
Pyramiderna
Jag lägger ingen aspekt på hur de använts eller byggts, jag fokuserar på matematiken bakom dem. Pyramider är matematiska kroppar med bestämda relationer mellan bredd och höjd.
Matematiken bakom dem och deras användningsområde står inte i strid med varandra. Faktiskt ansluter en egenskap hos gyllene snittet till begreppet 'uppståndelseapparat' som de gamla egyptierna kallade sina pyramider. Inverteras gyllene snittet så återuppstår det tillsammans med en etta.
1/G = 1 + G
Gyllene snittet som uppståndelsetal
Cheopspyramiden visar upp denna uppståndelserelation på sin yta.
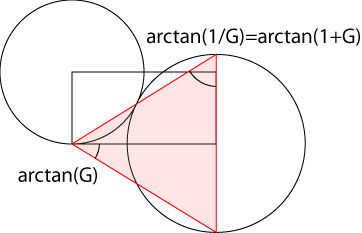
Cheopspyramidens yta visar upp gyllene snittets uppståndelseegenskap.
Talet 1 och gyllene snittet
Kjedjebråket av talet ett är lika med gyllene snittet. Under processen att skapa kjedjebråket av talet 1 framträder Fibonaccitalen.
1/1
1/(1+1/1)=1/2
1/(1+1/2)=2/3
1/(1+2/3)=3/5
1/(1+3/5)=5/8
1/(1+5/8)=8/13
...
I täljaren i bråken, överst, så framträder Fibonaccitalen.
Talserierna kopplade till gyllene snittet
Utifrån gyllene snittet, som vi ser i Cheopspyramiden, kan vi skapa Fibonaccitalen via potenserna av gyllene snittet och längden av diagonalen i 1:2-rektangeln.
Fibonaccitalen
Start vid G0: 0 1 1 2 3 5 8 13 21 34 55 ...
Start vid G1: 1 1 2 3 5 8 13 21 34 55 ...
Kvoterna som framträder här ovan kommer att närma sig gyllene snittet när vi går längre och längre i skapandet av kjedjebråket.
Uppståndelseegenskapen leder oss nu vidare:
1/G=1+G
Det betyder att 1/G-G=1.
Vi kan skapa heltal från relationerna:
1/GN-GN, där N är de udda heltalen.
1/GN+GN, där N är de jämna heltalen.
De tal vi nu får fram kallas Lucastalen.
Lucastalen
Start vid G0: 2 1 3 4 7 11 18 29 47 79 123 ...
Start vid G1: 1 3 4 7 11 18 29 47 79 123 ...
Oftast ser vi talserierna med starten vid G1. Vi ser att 10/89 skapas av Fibonaccitalen och 12/89 av Lucastelen i diagonelen i en kvadrat. Summerar vi dessa två tal får vi 22/89 vilket motsvarar skillnadsvinkeln för Chefrenpyramidens yttringales topp och Mykerinospuramidens genomskänings topp.
arctan(40/9)-arctan(2)=arctan(22/89)=arctan(10/89+12/89)
Vi kan nu se ytterligere en koppling mellan de två talseriena när vi studerar ytan på Cheopspyramiden.
Cheopspyramiden och talserierna
De två talserierna vi nu fått fram finns representerade på ytan av Cheopspyramiden på följande sätt då
arctan(G) kan skivas på följande sätt:
arctan(G) = arctan(G)+arctan(0/1) Fibonaccital
arctan(G) = arctan(G3)+arctan(1/3) Lucastal
arctan(G) = arctan(G5)+arctan(1/2) Fibonaccital
arctan(G) = arctan(G7)+arctan(4/7) Lucastal
arctan(G) = arctan(G9)+arctan(3/5) Fibonaccital
arctan(G) = arctan(G11)+arctan(11/18) Lucastal
arctan(G) = arctan(G13)+arctan(8/13) Fibonaccital
arctan(G) = arctan(G15)+arctan(29/47) Lucastal
arctan(G) = arctan(G17)+arctan(21/34) Fibonaccital
arctan(G) = arctan(G19)+arctan(76/123) Lucastal
...
Vi ser växelvis kvoter av Fibonaccital och Lucastal. Men vi ser även de udda potenserna av gyllene snittet.
De udda potenserna av gyllene snittet skapar en halva av Lucastalen.
|
1/G-G=1
1/G3-G3=4
1/G5-G5=11
1/G7-G7=29
1/G9-G9=76
1/G11-G11=199
1/G13-G13=521
1/G15-G15=1364
1/G17-G17=3571
1/G19-G19=9349
1/G21-G21=24476
1/G23-G23=64079
1/G25-G25=167761
1/G27-G27=439204
1/G29-G29=1149851
1/G31-G31=3010349
1/G33-G33=7881196
1/G35-G35=20633239
1/G37-G37=54018521
1/G39-G39=141422324
1/G41-G21=370248451
1/G43-G43=969323029
1/G45-G45=2537720636
1/G47-G47=6643838879
1/G49-G49=17393796001
1/G51-G51=45537549124
... |
Mönster
Tittar du noga ser du ett mönster i slutsiffran av talen, 141969.
Mönstret är 6 siffror långt. Vi kan se mönster i andra siffran från slutet och tredje siffran från slutet och så vidare. Mönsterlängderna beskrivs av 5N*6.
Ett dolt mönster
Det finns ett mönster till som är dolt vid första anblicken. Det mönstret framträder när vi tar talsumman för de tal vi nu fått fram. 142241857758, det mönstret är 12 siffror långt.
|
1/G-G=1 1
1/G3-G3=4 4
1/G5-G5=11 2
1/G7-G7=29 2
1/G9-G9=76 4
1/G11-G11=199 1
1/G13-G13=521 8
1/G15-G15=1364 5
1/G17-G17=3571 7
1/G19-G19=9349 7
1/G21-G21=24476 5
1/G23-G23=64079 8
1/G25-G25=167761 1
1/G27-G27=439204 4
1/G29-G29=1149851 2
1/G31-G31=3010349 2
1/G33-G33=7881196 4
1/G35-G35=20633239 1
1/G37-G37=54018521 8
1/G39-G39=141422324 5
1/G41-G41=370248451 7
1/G43-G43=969323029 7
1/G45-G45=2537720636 5
1/G47-G47=6643838879 8
1/G49-G49=17393796001 1
1/G51-G51=45537549124 4
... |
Spegling
När vi ser mönstret kan vi betrakta det som delat i 4 grupper med 3 tal i varje.
142 241 857 758
Vi ser direkt att 142 speglas till 214 och att 857 speglas till 758.
De 'ospeglade' 142 857 motsvarar samma mönster som vi finner i decimalutvecklingen av talet 1/7.
1/7 = 0,142 857 142 857 142 857 142 857 142 857 142 857 142 857 142 857 ...
Vi har nu fått fram talet 1/7 från talet 1 som kjedjebråk.
Vi kan nu skapa en vinkel på detta sätt från talet 1 och 1/7.
arctan(1)+arctan(1/7)
Grundmönstret hade 4 grupper med 3 siffror i varje grupp, nu visar det sig att:
arctan(1)+arctan(1/7)=arctan(4/3)
arctan(1)+arctan(y/x)
Vi ska se att arctan(1)+arctan(x) användts för fler pyramider. Entalsumman för mönstret är 9.
Genomskärningstrianglar arctan(1)+arctan(1/7) = arctan(4/3) Chefrenpyramiden
arctan(1)+arctan(1/9) = arctan(5/4) Mykerinospyramiden
Yttrianglar
arctan(1)+arctan(1/4) = arctan(5/3) Chefrenpyramiden
arctan(1)+arctan(G3) = arctan(1/G) Cheopspyramiden
arctan(1) uttryckt med radianer är Pi/4, som vi även som en relation fann hos cirkeln som inskrivs i kvadraten.
Vi ser även att samma vinkel skapas av 2(arctan(1/G)-arctan(G)). Yttriangeln hos Cheopspyramiden beskrivs av vinklarna arctan(1/G) vid basen och 2arctan(G) vid toppen.
Vi har därmed en symbol för det dolda mönstret vi funnit på djupet i gyllene snittet.
Symbolen för mönstret och gyllene snittet
Vi kan skapa en annan triangel baserat på gyllene snittet som när den skapas även ger symbolvinkeln för det dolda mönster vi funnit på djupet i gyllene snittet.
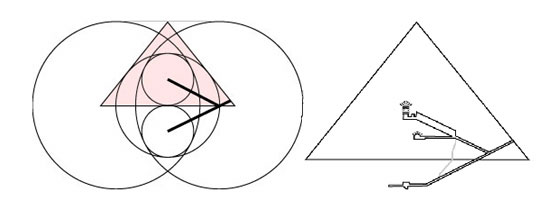
Cheopspyramidens genomskärningstriangel, arccos(G), och symbolvinkeln för mönstret vi fann på djupet i gyllene snittet. I Cheopspyramiden symboliseras det av gångsystemet som vi finner på djupet i själva pyramiden.
Vinkeln i denna triangel är arccos(G). Arccosinus kräver kunskaper om Pi då den baseras på cirkeln. Vi har redan sett hur den symbolvinkel vi nu fått fram även finns i Chefrenpyramidens genomskärningstriangel och hur den triangeln även är kopplad till Pi via 4/Pi.
Perfekt matchning
Men vi ser att matchningen inte är perfekt här. Pyramiden ser ut att vara längre från kanten till gångarnas skärningspunkt. Även basen är förskjuten längre ner.
Nu visar det sig att 142 241 857 758 och med grundkonstruktionen i kvadraten ger förklaringen. Låter vi cirkelkonstruktionen ovan anpassas till gyllene snittet i kvadraten så ser vi att modellen av den verkliga Cheopspyramiden är 4/3 gånger större. Den är förskjuten nedåt med 1/12 av lilla nedre cirkeln och förstorad så att avståndet mellan gångarnas skärningspunkt och sidan av pyramiden motsvarar 1/6 av pyramidens sida.
4/3 * 1/12 *1/6 = 1/54
54 får vi om vi summerar talen i mönstret.
1+4+2+2+4+1+8+5+7+7+5+8 = 54
Att det verkligen är gyllene snittet och mönstret som ligger till grund för Cheopspyramiden är nu tydligt.
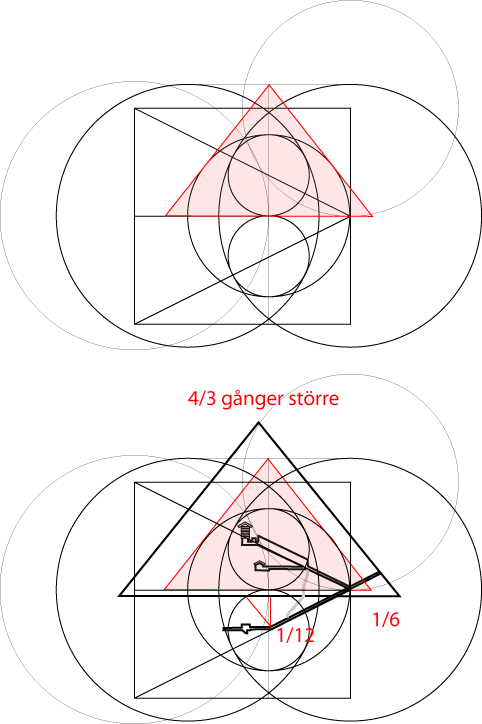
Anpassningen till den verkliga modellen för Cheopspyramiden ger talen 4/3, 1/12 och 1/6. Dessa tal återkopplar till summan av talen i mönstret, 54. Vi har därmed en återkopplingen som bekräftar att mönstret pekas ut. När vi lägger in cirkelkonstruktionen kommer skärningen mellan cirklarna att ligga roten ur 4*G3 upp längs rektangeln. Vinkeln mellan gångarna och Chefrenpyramiden kan också beskrivas som 4arctan(G3).
Mönstret av 12 siffror där 6 av dem kopplas till vinkeln som beskrivs av arctan(4/3). Mönstret kan ses bestå av 4 grupper med 3 siffror i varje. Genom att kombinera dessa tal så att 54 framträder så bekräftas att det är mönstret som pekas ut då 54 även talsumman för de ingående siffrorna i mönstret. Cheopspyramiden är på detta sätt en vägvisande konstruktion.
Vi har redan i introduktionen sett hur Chefrenpyramiden kopplas till mönstret. Pyramiden som står strax söder om den är Mykerinospyramiden och dess genomskärningstriangel har basvinkeln arctan(5/4).
Entalstalsumman av mönstret är:
1+4+2+2+4+1+8+5+7+7+5+8 = 54, 5+4=9
Mykerinospyramidens vinkel i gyllenen vinkelrelationen
arctan(1)+arctan(1/9) = arctan(5/4)
Trappstegspyramiden i Sakkara
54 som ett mönster är också kopplat till trappstegspyramiden. Den är 6 trappor hög och detta delar basen i 11 delar. Trappstegspyramiden är den första som byggs.
6/11 = 0,54 54 54 54 54 54 54 54 54 54 ...
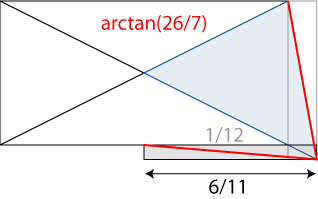
6/11 framträder när Chefrenpyramiden skapas på detta sätt i 1:2-rektangeln. En 1:12-rektanglen framträder då och vinkeln arctan(26/7). 26 är ett tal vi kommer att se åkerkopplar Chefrenpyramiden till gyllene snittet, se under fliken 'I skrift'.
4/7 och 57
Vi har sett hur relationen 4/7 skapas från Chefrenpyramiden i kvadraten när 1:7-rektangeln skapar den,
4/7=(57+1/7)/100. Talet 57 framträder nu med i konstruktionen ovan. vi ser en 2:11-rekatngel med en 1:5-rektanglen i sig vid 1:2-rektangelns högra kant. Vinkelnskillnaden i diagonalerna där är arctan(1/57).
Vi kommer längre fram att se hur talet 26 tillsammans med talet 31 skapar en djupare koppling mellan Cheopspyramdien och Chefrenpyramiden. Vi kommer i det sammanhanget att se att 31 även är kopplat till 1:2-rektangeln. Summerar vi de två talen 26+31=57.
Nu visar det sig att i Sakkarapyramidens inre finns en till trappstegspyramid, 4 trappor hög som delar sidan i 7 delar, 4/7 alltså.
Kopplingen mellan 26 och 31 via Gyllene vinkelrelationen ger kopplingen till talet 5 och 57. Talet 19 kopplas till detta på samma sätt som 1/89 kopplas till Fibonaccitalen. Dessutom ger Lucastalen 19*(1/89). Via femstjärnan och Gyllene vinkelrelationen kommer G3 att pekas ut. Vi ser nu att 360/(12+1/19) som breddgrad går genom gården söder om pyramiden och toppen ligger vid 360/(12+1/(19+G3)) när förskjutningen på 68 meter tagits med.
Du finner pyramiden i Google Earth vid: 29 52 16N 31 12 58E
Meidumpyramiden
3/11 skapar ett mönster av 27. 27 är talsumman för mönstret i 1/7.
3/11 = 0,27 27 27 27 27 27 27 27 27 27 ...
Vi fann ju detta mönster på djupet när vi utforskade gyllene snittet. Via talet 1's kjedjebråk fick vi fram Fibonaccitalen och sedan gyllene snittet.
1+3/11=14/11
Vinkeln i Meidumpyramiden är arctan(14/11).
Inne i Meidumpyramiden finns två trappstegspyramiden den ena med 8 trappo och den inre med 7 trappor. Vi ser nu dirket att arctan(8)-arctan(7)=arctan(1/57).
Dessutom finner vi att arctan(1/8)+arctan(1/8)=arctan(3/11).
Placeringen av Maidumpyramiden
Talet 4 återfinner vi både i Chefrenpyramiden och Cheopspyramiden. I Cheopspyramiden är det via kjedjebråket av talet 4.
1 och 3/11 kopplas till talet 4 via talet 7. Det är via vinkalr igen som skapar denna koppling.
arctan(1) + arctan(3/11) = arctan(7/4)
arctan(1) - arctan(3/11) = arctan(4/7)
Grundkonstruktionen av Chefrenpyramiden via kvadraten ger kopplingen till 4/7 och 7/4.
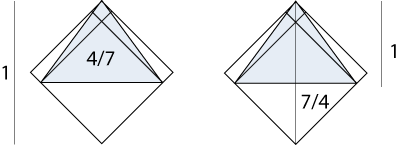
Relationerna 4/7 och 7/4 via Chefrenpyramiden och kvadraten.
Vi vet även att den tredimensionellan toppen av Chefrenpyramiden beskrivs av arctan(4)-arctna(1/4). Yttrianglen hos Chefrenpyramdien beskirvas av arctan(5/3)=arctan(1)+arctan(1/4). Vi ser nu även hur Chefrenpyramiden i 1:2-rektangeln kommer att ge talet 1/4 när Meidumpyramiden konstrueras.
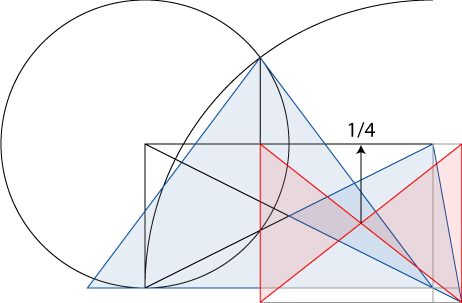
Chefrenpyramiden, blå, på två sätt ger Meidumpyramiden, röd, och pekar på talet 1/4 i 1:2-rektangeln. Detta kommer att peka ut pyramidens breddgrad.
Tittar vi på Cheopspyramiden är det istället kjedjebråket av talet 4 som kopplas till pyramiden, arctan(1/G)=
arctan(1)+arctan(4kj). Även femstjärnan är kopplad till kjedjebråket av talet 4 som är lika med G3.
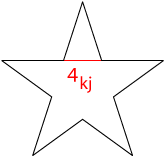
Femstjärnan koppling till talet 4 via kjedjebråk.
Cheopspyramidens ytter har vinkeln arctan(1/G). Genomskärningstriangelns topp beskrivs av arccos(G3).
Arctan(1/G) = arctan(1) + arctan(4kj)
Arctan(G3) = arctan(4kj)
Breddgraden för Meidumpyramiden är 360/(12+1/4) = 29o 23' 15,92''
Du kan kontrollera själv med Google Earth. Vi lägger då på samma kontinentalförflyttning norrut som för Cheopspyramiden, 68 meter.
360/(12+1/4) + 68 meter = 29o 23' 18,1''
Kopiera detta, N29 23 18 E31 9 27, och klistra in i ruta 'Ta mig till' i Google Earth så tas du till Meidumpyramdien och kan kontrollera själv. Tänk på att Meidumpyramiden har rasat till stora delar, avgöra mittan av rasmassorna och du ser att det stämmer.
Vi vet nu också att talet 4 kopplas till relationen som kopplas till Pi, 4/Pi. Talet 4 finner vi i vinklarna för både Cheopspyramiden och Chefrenpyramiden. Vi fann även att talet 1/38 kopplade de två pyramiderna. Nu visar det sig att samlingstalet för Gyllene vinkelrelationen baserad på 14/11, Meidumpyramiden, är 38/89.
Dashurpyramiderna
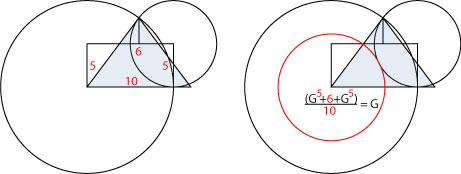
10 5 6 5 i samband med Chefrenpyramidens konstruktion i samband med att gyllene snittet, G, framträder.
Ekvationen
Vi ser nu hur talen 10 5 6 5 kopplas till en ekvation som har en lösning i G.
(x5+ 6+ G5 )/10) = x
Utforskar vi den ekvationen ser vi att relationen 7/5 framträder, den relationen ger basvinkeln för Brutna pyramiden, arccos(7/5). Den ändrar vinkel en bit upp längs sidan, den nya vinkeln är givetvis kopplad till det vi nu vet.
Vi börjar med ekvationen och dess koppling till femstjärnan och en konstruktion av Chefrenpyramiden. Vi ser här ekvationen plottad mellan x=-2 och x=2. Vi ser då relationerna 7/5 och 3/5. 3/5 är relationen som gav talen 10 5 6 5. Arccos(3/5) är även vinkeln i Chefrenpyramiden. Arccos kan ses kopplat till Pi och vi finner vinkeln i femstjärnan som (3/5)*Pi radianer.
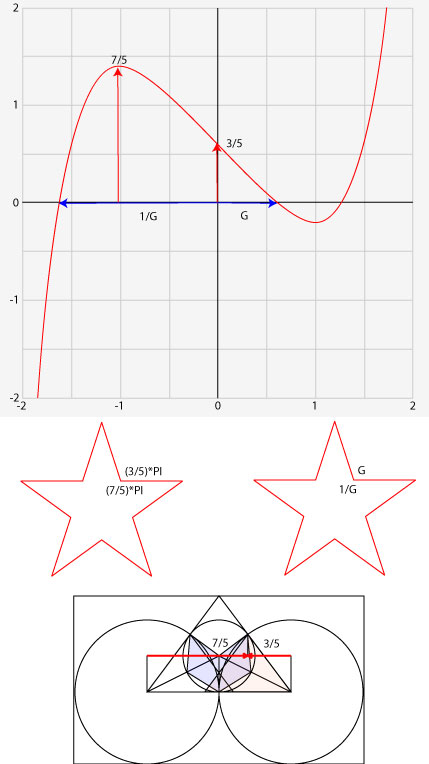
G och 1/G finner vi i yttriangeln för Cheopspyramiden. 3/5 är relationen som ger ekvationen och Chefrenpyramidens vinkel via cirkeln, arccos(3/5). Relationen 7/5 finner vi även i basvinkeln hos Brutna pyramiden vid Dashur. Men vi finner även 7/5 i en konstruktion av Chefrenpyramiden. Denna konstruktion är intressant då den innesluts i en 7:12-rektangel. Vi minns de 12 siffrorna som dolde inversen av talet 7. Klipper vi ut den blå ytan och viker på mitten och längs diagonalerna i 1:2-rektangeln så får vi den tredimensionella Cheopspyramiden. Diagonalerna i 1:2-rektangeln har längden 1/G+G, eller roten ur 5.
Vi finner en annan koppling till Brutna pyramidens relation 7/5 när relationen 4/(3+G) delas upp efter Chefrenpyramiden. Röda strecket nedan är 7/5-2/Sqr(5), senare kommer den att beskrivas som (5+G6)/10 i samband med Anundshög i Sverige, då tas även 4/(3+G) upp. 2/Sqr(5) kommer att visa sig ge kopplingen mellan Brutna pyramidens topp och Röda pyramiden.
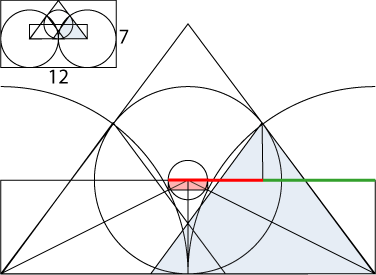
Nya vinkeln
Brutna pyramiden har fått sitt namn av att dess vinkel ändras en bit upp längs sidan. Vi ska se på hur vi skapar Cheopspyramiden och Chefrenpyramiden från kvadraten för att förstå den nya vinkeln. Den är arctan(4*G3), vi ser en symbolisk koppling till Chefrenpyramdiens vinkel som kan beskrivas som 4arctan(G3).
Om vi omsluter konstruktionen får vi att omslutande rektangeln har relationen 4*G3.
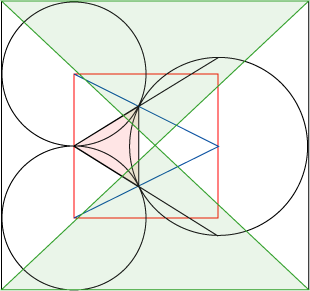
Den röda trianglen är Cheopspyramidens yttriangle och de blå motsvarar gångsystemet och Chefrenpyramiden. De gröna trianglarna har vinkeln arctan(4*G3), som toppen på Brutna pyramiden.
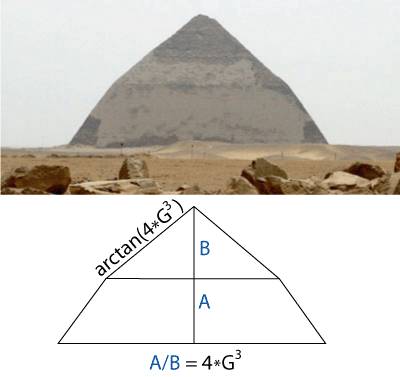
4*G3 skapar vinkeln i övre delen av Brutna pyramiden. 4*G3 har även använts för var pyramiden byter vinkel.
Brutna pyramidens breddgrad
Vi kan konstruera Brutna pyramiden i grundkonstruktionen där 10 5 6 5 framträder. Vi ser då att hela Chefrenpyramiden i den konstruktionen är 12 lång. Vi kan konstruera Brutna pyramidens basvinkel via den konstruktionen. Vi lägger dirket märke till att breddgraden 360/(12+1/12) går mellan de två Dashurpyramiderna.
Samarbete mellan cossinus och tangens beskriver både pyramider och kjedjebråk.
Om genomskärningstrianglen i en pyramid beskriva med arccos(X) så är yttrianglens vinkel arctan(1/X). Vi inser med detta att sexstjärnans 60 garder också är kopplad till Cheopspyramidens yttre, arccos(1/2)=60. X=1/2 ger 1/X=2 och yttre toppvinkeln på Cheopspyramiden har vinkeln arctan(2) som är lika med 2*arctan(G).
Rektangeln X:2 ger kjedjebråket för talet X, Xkj = 1/(cos(arctan(X/2)) - X/2
Från samma bas kan vi skapa Cheopspyramiden som visats tidigare. Gyllene snittet är även lika med kjedjebråket för talet 1, G = 1kj. Geometriskt kan vi konstuera kjedjebråket av ett tal via en rektangel. Rektangeln X:2 där X är talet vi ska skapa kjedjebråker för. Vi ser nu att Brutna pyramiden koppllas till 5:2-rektanglen i vår konstruktion.
Toppen pekar därmed på kjedjebråket för talet 5. I kontruktionen inser vi nu att 12-5kj framträder. Med kontinentförflyttningen på cirka 68 meter får vi då pyramiden byggdes på breddgraden 360/(12+1/(12-5kj)). Du kontrollerar lätt själv med Google Earth, 360/(12+1/(12-5kj)) = 29o 47' 23,11''
Med samma förflyttning norr ut som Cheopspyramiden ger den nuvarande breddgraden:
360/(12+1/(12-5kj)) + 68 meter = 29o 47' 25,3''
Med Google Earth kan du skriva in N29 47 25 E31 12 34, och du tas till Brutna pyramiden och kan kontroller breddgraden själv. Tänk på att pyramiden är fotad lite från sidan så mät vid pyramidens bas.
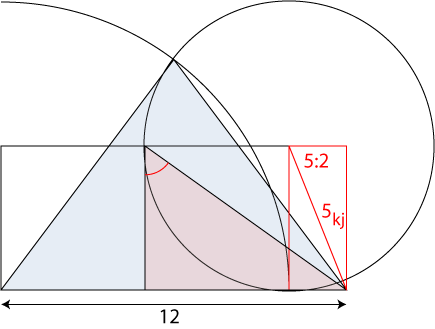
Geometriska konstruktionen av Brutna pyramidens basvinkel som pekar på 12-5kj som ger dess breddgrad.
Vi ser nu en koppling till mellan Chefrenpyramiden och Brutna pyramiden. Toppvinkeln i Chefrenpyramiden kan beskrivas som arccos((7/5)*(1/5)). 7/5 ger vinkeln i Brutna pyramiden. Talet 5 via kjedjebråk ger breddgraden för pyramiden. Vi har även en symbolisk återkoppling till gyllene nsittet och Chefrenpyramidens 10 5 6 5 då det är kjedjebråker av talet 1.
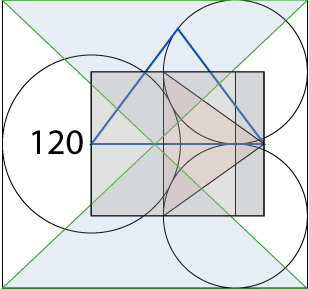
120
Talet 120 kopplar sig till Brutna pyramiden i gyllene snittkonstruktionen. Gör vi så att Chefrenpyramiden i konstuktionen ska beskrivas av heltal i sin koppling till ursprungliga 1:2-rektangeln blir grå rektanglens yta 10*12=120.
Röda pyramiden
1:2-rektangel kopplar sig till 4*G3 på så sätt att relationen mellan diagonalen, 1/G+G, och basen som:
(1-G6)/(1+G6) = 2/Sqr(5)
Vi ser då att (1-G6)=4*G3
Vi kan skriva (1-G6)/(1+G6)=(4*G3)*(1/(1+G6))
Vinkeln i Röda pyramiden är arctan(1/(1+G6))
Vi kan skapa den vinkeln genom att utgå från skärningspunkten i kvadraten där Cheopspyramiaens triangel skär Chefrenpyramidens vinkel. Vi lägger in en cirkel som har radien som den som de små cirklarna från början.
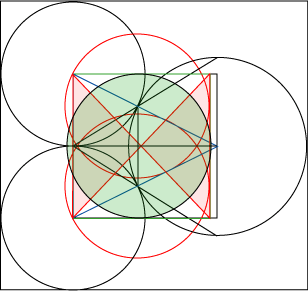
Röda pyramidens triangel motsvarar den röda trianglarna i bilden. Vinkeln i den är arctan(1/(1+G6)). Denna vinkel kopplar sig djupare till Cheopspyramiden och talet 1/7. Den gröna cirklen är förskjuten exakt lika mycket som de röda och är med att skapa Röda pyramidens vinkel. Den gröna cirkeln kommer att ge breddgraden för skeppssätningen vid Anundshög i Västerås när vi förstått förskjutningen fullt ut.
1/7 och Röda pyramiden
Vi har sett hur arctan(G) i Cheopspyramiden kan skrivas som en serie av vinklar baserade på Fibonaccirelationer och Lucasrelationer tillsammans med de udda potenserna av gyllene snittet.
arctan(G) = arctan(G)+arctan(0/1) Fibonaccital
arctan(G) = arctan(G3)+arctan(1/3) Lucastal
arctan(G) = arctan(G5)+arctan(1/2) Fibonaccital
arctan(G) = arctan(G7)+arctan(4/7) Lucastal
arctan(G) = arctan(G9)+arctan(3/5) Fibonaccital
arctan(G) = arctan(G11)+arctan(11/18) Lucastal
arctan(G) = arctan(G13)+arctan(8/13) Fibonaccital
arctan(G) = arctan(G15)+arctan(29/47) Lucastal
arctan(G) = arctan(G17)+arctan(21/34) Fibonaccital
arctan(G) = arctan(G19)+arctan(76/123) Lucastal
...
Det vet ju att grundmönstret, 142 241 857 758, bär mönstret i 1/7, 142 857.
Summerar vi just de G-potenser som skapar mönstret i 1/7 och summerar dem får vi, 1/(1+G6).
G + G3 +G5 + G13 + G15 + G17 + G25 + G27 + G29 + G37 + G39 + G41 + ... = 1/(1+G6)
Röda pyramiden bekräftar därmed att det är just 1/7 som är viktig i samband med gyllene snittet.

|